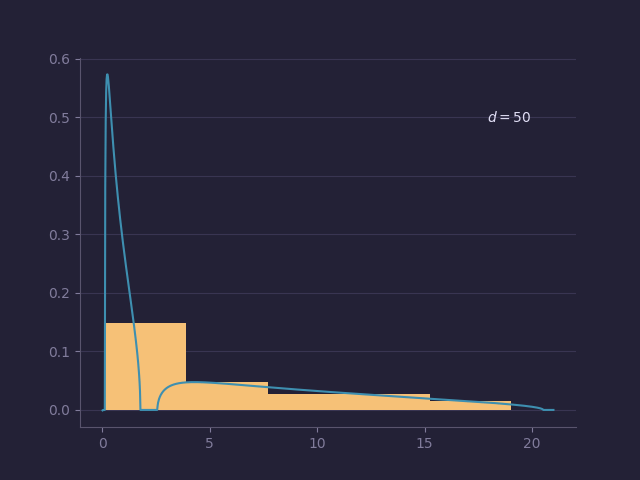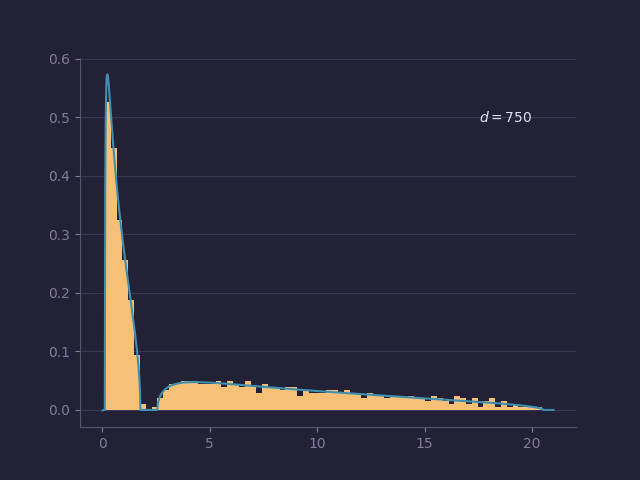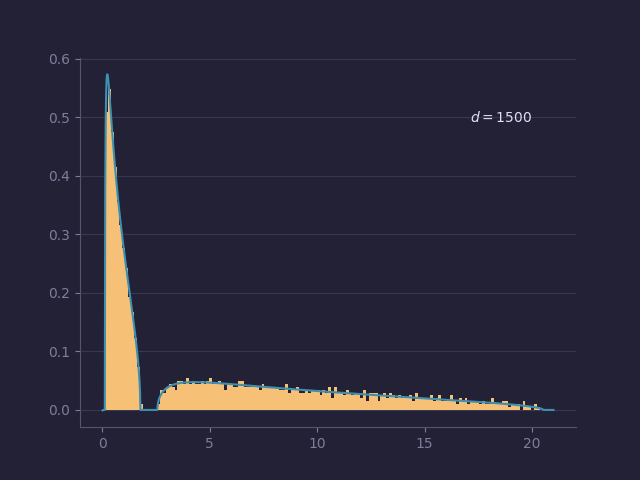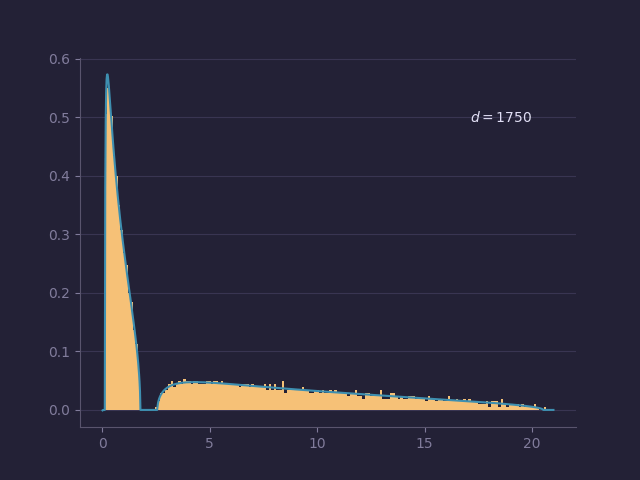
Random matrix theory | Hugo Latourelle-Vigeant

How, and when, can we describe the asymptotic spectral information of random matrices? To what extent do random matrices depend on the distribution of their entries?

I am broadly interested in spiked models, phase transitions, universality, and applications to data science and machine learning. The field brings together a diverse toolbox (leave-one-out methods, concentration inequalities, Stein’s method, and ideas from free probability) and operates at multiple levels of precision, from global laws to mesoscopic and local regimes. I am particularly interested in how these techniques can be extended to structured models such as linearizations and correlated pencils, and more generally in adapting classical tools to settings motivated by modern high-dimensional problems.

The empirical spectral distribution of a covariance matrix converges as the dimension of the matrix increases. We observe two distinct bulk in the high-dimensional limit, hinting at the structure of the underlying covariance matrix.