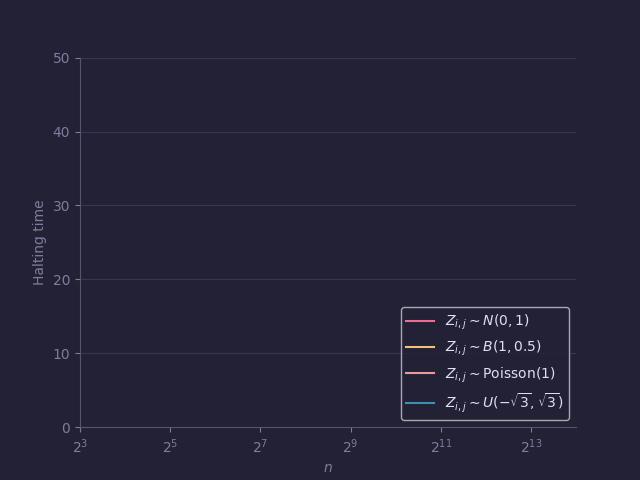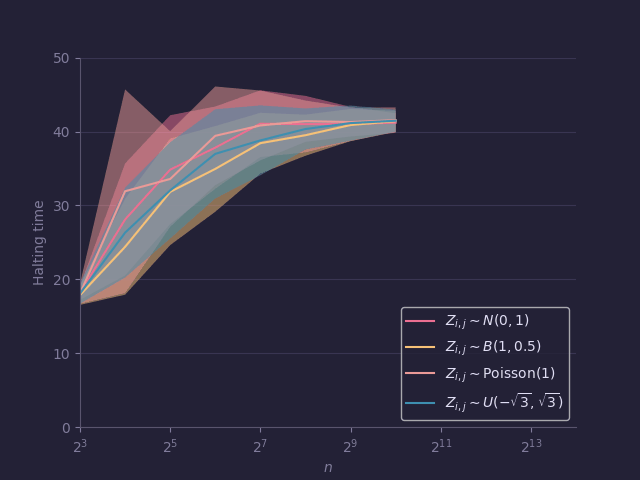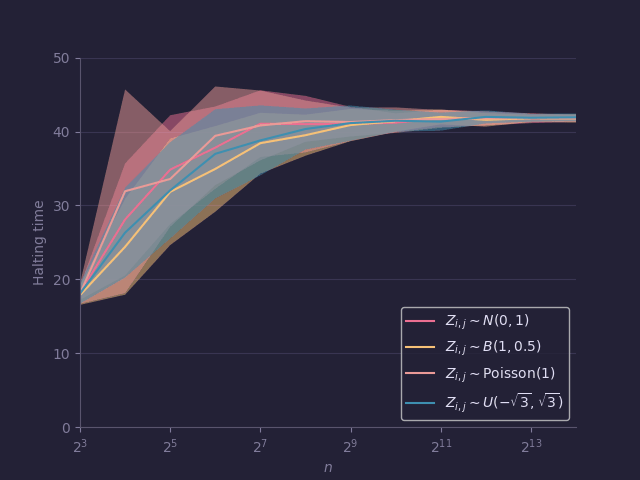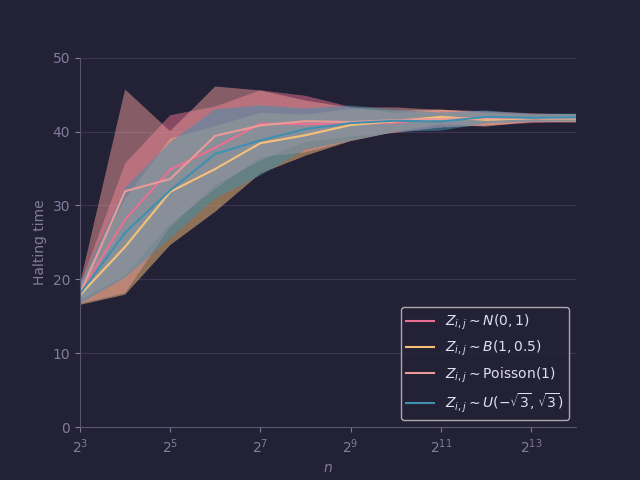
Dynamics of training

What the relation between properties of the data, such as its probability distribution and the presence of low-rank signals, and the behavior of optimization algorithm? What is the average-case complexity of optimization algorithm in the large-scale setting?

In high-dimensional learning problems, optimization algorithms exhibit rich and sometimes unexpected behaviors. The interaction between data distribution, noise, and low-rank structure can strongly shape training trajectories, and random matrix methods help reveal universality phenomena that persist across models. For large problems, worst-case complexity often fails to capture typical behavior, and average-case analyses provide more relevant insight, especially when universality makes performance largely independent of fine distributional details. Beyond finding a minimizer, training can introduce inductive biases that improve generalization in over-parameterized models, and learning may unfold in a stage-wise or “staircase” manner, with relevant directions discovered sequentially.