Tutte embedding
An interactive visualization of Tutte's embedding algorithm for planar graphs.
Motivation
I was taking the course Spectral Graph Theory at Yale University, taught by Professor Dan Spielman. When we first discussed planar embeddings of graphs, he briefly mentioned this site. The premise is simple: you’re given a random planar graph, and you need to find a planar embedding by dragging the vertices around. You can choose the number of vertices, and there’s a timer to track how long it takes you to solve it. I played around with it for a bit.
For small planar graphs, it seemed pretty manageable, but as the number of vertices increased, it quickly became challenging.
Tutte’s Theorem
Later in the same course, we discussed Tutte’s theorem. Given a 3-connected planar graph, a Tutte embedding is a drawing of the graph where the outer face forms a convex polygon, and the inner vertices are placed harmonically. Here, by “placed harmonically,” we mean that the position of each inner vertex is the average of its neighbors. The theorem states that such an embedding is always planar.
More precisely, suppose that
- \(G = (V, E)\) is a 3-connected planar graph with \(n\) vertices,
- \(V \subseteq \mathbb{R}^2\) is the set of vertices, and
- \(E\) is the set of edges.
Assume that we can (for some reason) determine the vertices of the outer face of the graph, which we denote by \(B\) (for boundary). We then fix the positions of these vertices in a convex polygon.
We still need to place the inner vertices. An intuitive way to think about Tutte’s embedding is through a physical lens: suppose that all edges in the graph act as ideal springs. We nail the outer face of the graph to a wall. To find the Tutte embedding, we could simply let go of the inner vertices and allow the springs to reach equilibrium.
This equilibrium corresponds to a harmonic embedding of the inner vertices \(S = V \setminus B\). The force exerted by a rubber band between vertices \(i\) and \(j\) on vertex \(i\) is \(v_j - v_i\), where \(v_i\) is the position of vertex \(i\). The equilibrium is reached when the net force on each inner vertex is zero. That is, we seek a solution to
\[\begin{align*} \sum_{j \in N(i)} (v_j - v_i) = 0 \quad \Rightarrow \quad v_i = \frac{1}{d_i} \sum_{j \in N(i)} v_j \end{align*}\]where \(N(i)\) is the set of neighbors of vertex \(i\), and \(d_i\) is the degree of vertex \(i\).
Using matrix notation, let \(M\) be the adjacency matrix of the graph, \(D = \text{diag}(d_1, \ldots, d_n)\) the degree matrix, and \(L = D - M\) the Laplacian matrix. Then, we can rewrite the equilibrium condition as
\[\begin{align*} L_{S,S}\, v_S = M_{S,B}\, v_B. \end{align*}\]The matrices \(L_{S,S}\) and \(M_{S,B}\) are the submatrices of \(L\) and \(M\) indexed by the inner and outer vertices. Since \(v_B\) is fixed and \(L_{S,S}\) is positive definite whenever \(\emptyset \subset B \subset V\) (note the strict inclusion), the above equation has a unique solution for \(v_S\).
Updating the inner vertices to \(v_S\) gives us the Tutte embedding of the graph, which we know is planar by Tutte’s theorem.
Implementation
I found Tutte’s theorem to be quite a nice result, and I wanted to see it in action. To make myself feel better about my poor planar drawing skills, I decided to implement the algorithm using React and JavaScript. This was also a great opportunity to try hosting a small interactive visualization on a GitHub page. The code is available on my GitHub repository. It’s not in the bestest of shapes, but it works for now.
If we ignore the logic for handling user input, the main part of the algorithm follows these steps:
Step 1: Generate a random (probably) 3-connected planar graph
To generate a random 3-connected planar graph, we start by placing a set of points uniformly at random within a square. We then compute the Delaunay triangulation of these points, which results in a planar graph. By construction, the convex hull of the points forms the outer face of the graph. We shuffle the vertices.
Step 2: Fix the outer face
The user can drag vertices or double-click on them to mark them as fixed (part of the outer face). Alternatively, they can click a button to automatically identify and fix the outer face.
Step 3: Animate the inner vertices
The core of the algorithm is the animation of the inner vertices, updating their positions according to the harmonic embedding equation.
nodes.forEach(node => {
// If the node is fixed, skip it
if (node.color === 'black') return;
// Find the neighbors of the node
const neighbors = graphData.edges
.filter(edge => edge.from === node.id || edge.to === node.id)
.map(edge => (edge.from === node.id ? edge.to : edge.from));
// Compute the target position of the node
const target = neighbors.reduce(
(acc, neighborId) => {
const neighbor = nodes.find(n => n.id === neighborId);
acc.x += neighbor.x;
acc.y += neighbor.y;
return acc;
},
{ x: 0, y: 0 }
);
// Average the positions of the neighbors
target.x /= neighbors.length;
target.y /= neighbors.length;
// Compute the force exerted on the node
const force = { x: target.x - node.x, y: target.y - node.y };
// Update velocity and position using a "momentum" term
node.vx = (node.vx || 0) * 0.8 + force.x * 0.2;
node.vy = (node.vy || 0) * 0.8 + force.y * 0.2;
// Update the position of the node
node.x += node.vx;
node.y += node.vy;
});
This is a simple implementation of the equation from the previous section. Instead of directly solving the linear system, we use an iterative approach with momentum to update the positions of the inner vertices. This simulates the behavior of springs finding their equilibrium by initially overshooting and then oscillating around the target position before settling.
Once a planar embedding is found, the color of the inner vertices changes to pink.
Results
You can play around with the code here. Otherwise, here’s an animation of the code in action.
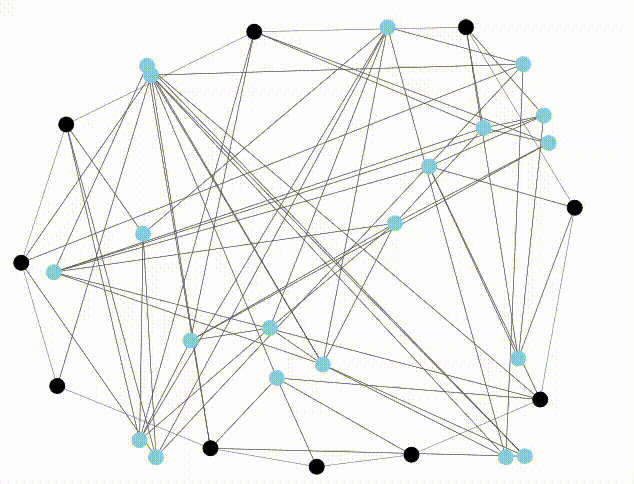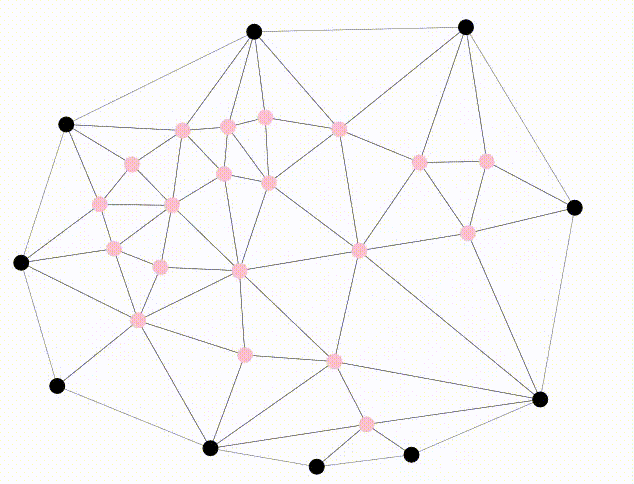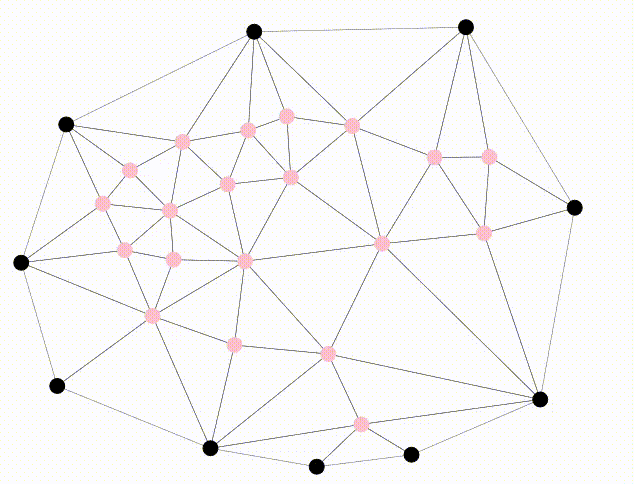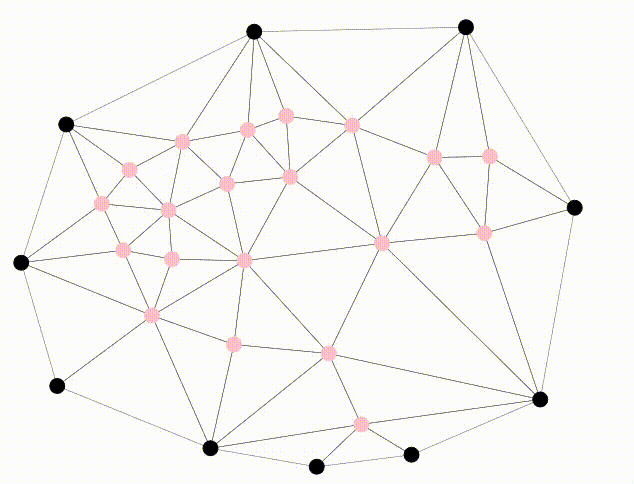
References
For more details on Tutte’s theorem and other interesting results in spectral graph theory, I encourage you to check out the draft of Spectral and Algebraic Graph Theory by Daniel A. Spielman.